https://www.acmicpc.net/problem/11729
하노이의 탑 입니다. 문제의 조건은 다음과 같습니다.
1. 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
2. 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
최소 이동으로 가는 횟수와 옮기는 과정을 구해야 합니다.
직관적으로 생각해봅시다.
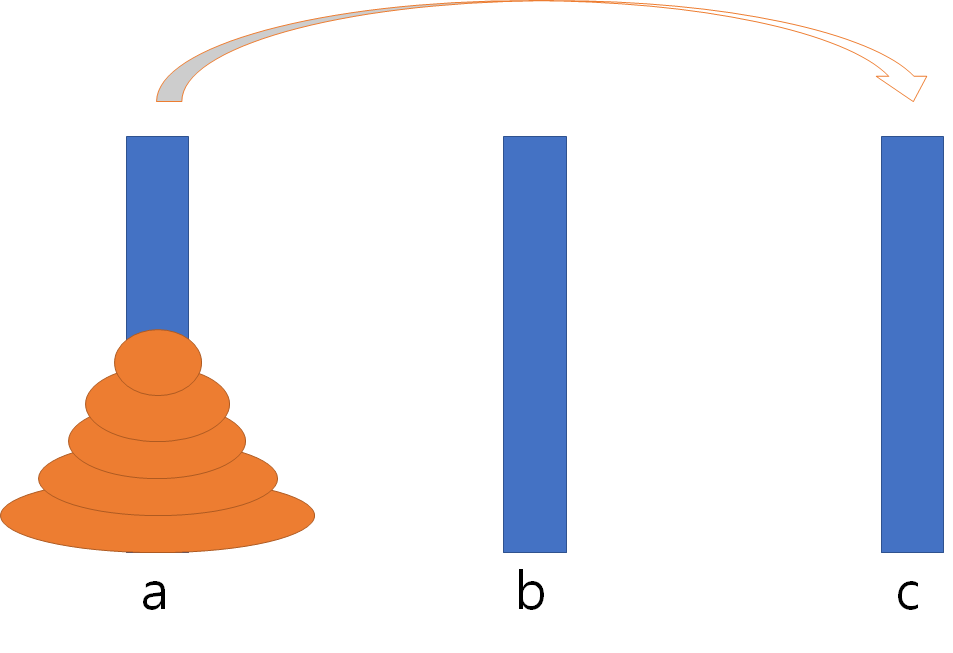
위와 같이 a기둥에 n개의 원판이 주어지고 이 원판들을 모두 c로 옮겨야 합니다.
이 원판을 조건에 맞게 옮기려면 일단 아래 깔린 가장 큰 원판부터 c로 옮겨야 합니다.
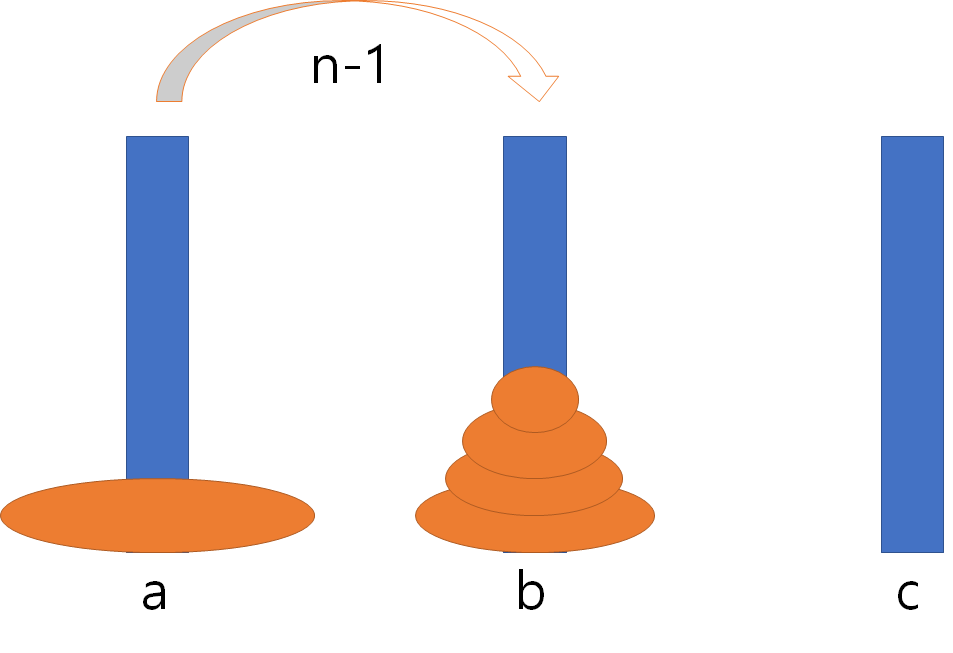
그러기 위해선 위와같이 a에 있는 n-1개의 원판을 b로 먼저 옮겨줘야겠죠? (어떻게 옮길진 아직 생각 않으셔도 됩니다. 아몰랑)
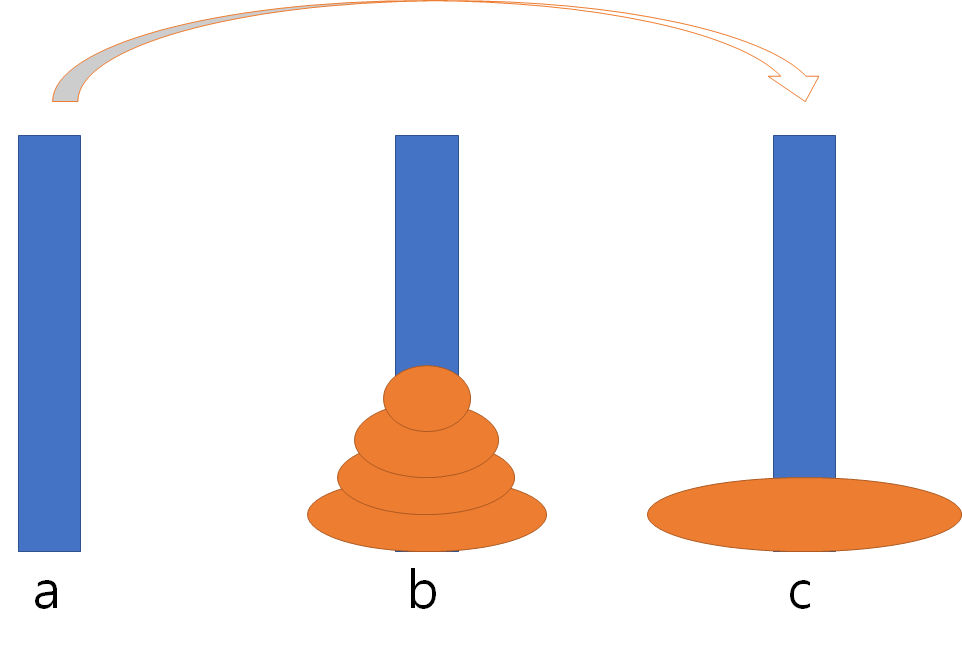
그 다음 a에 남은 가장 큰 원판을 c에 옮겨주고
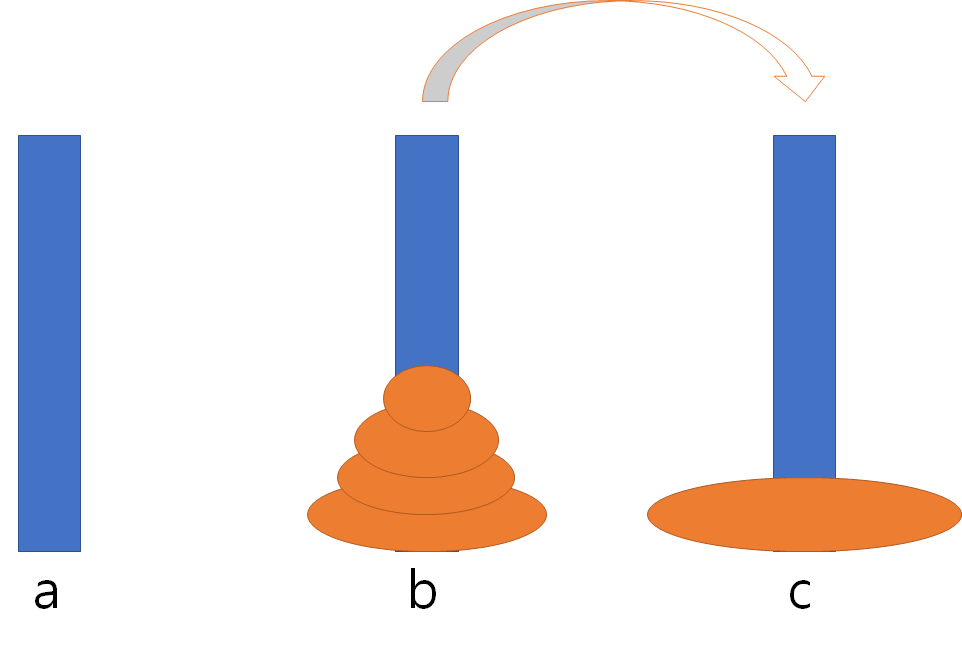
이제 남은 b에 남은 모든 원판들을 c로 옮겨주면 됩니다. (처음 a에서 c로 옮기는 과정처럼 하면 되겠죠?)
일단 직관적으로 생각한 것을 코드로 옮겨보겠습니다.
python3 코드
from sys import*
setrecursionlimit(10**6)
def move(_from, to):
global ans
ans.append((_from, to))
def hanoi(n, a, b, c): #원판개수, from, by, to
if n==1: #base case 원판 하나이면 a->c로 옮기고 끝냄
move(a, c)
return
hanoi(n-1, a, c, b) #n-1개를 a->b로 이동
move(a, c) #남은 가장 큰 원판 a->c로 이동
hanoi(n-1, b, a, c) #위에서 옮겨놓은 n-1개를 b->c로 이동
n=int(input())
ans=[]
hanoi(n,1,2,3)
print(len(ans))
for a, c in ans:
print(a, c)
hanoi(n, a, b, c)는 각각 n=원판의 개수, a=from, b=by, c=to 입니다.
즉, 두번째 오는 인자가 원판이 옮겨질 기둥이고, 네번째 오는 인자가 원판을 옮길 기둥 입니다.
이 함수의 실행과정을 각각의 예를 들어 살펴보겠습니다.
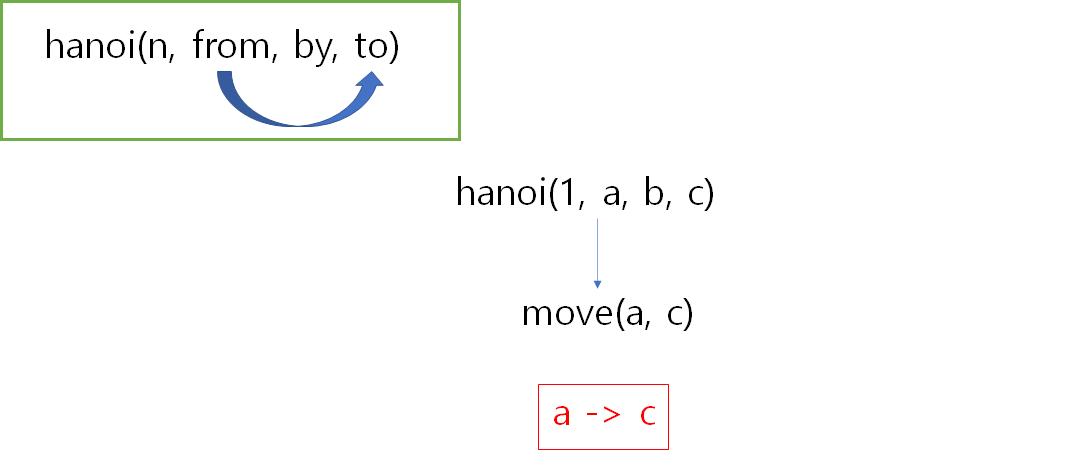
n==1입니다.
hanoi(1, a, b, c) 가 호출 되면 n==1인 base case에 걸려서 move(a, c)를 호출하게 되고, 원판을 a->c로 보내고 끝나게 됩니다.
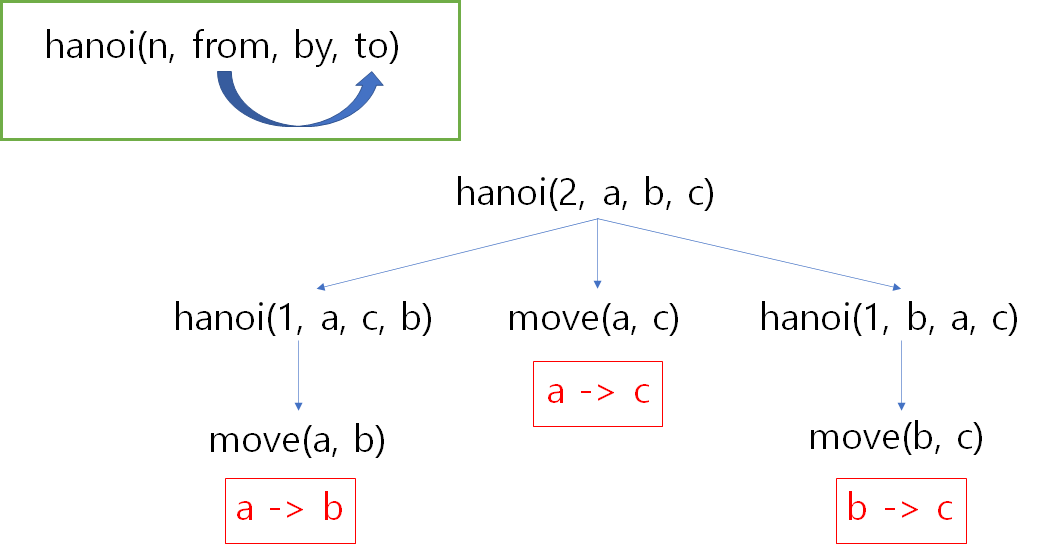
다음은 n==2 입니다.
hanoi(2, a, b, c)가 호출 되고,
이 함수는 hanoi(1, a, c, b)를 호출하고, 이 함수는 n==1이라 move(a, c)를 실행 합니다. 근데! 여기서 호출된 함수의 순서가 1, a, c, b 입니다. 즉, 두번째인자(from)에 있는 옮길 기둥이 a, 네번째인자(to)에 있는 옮겨질 기둥이 b이므로 결과적으로 a -> b로 이동하게 됩니다.
그 후 move(a, c)가 호출 되는데, 이 때는 hanoi(2, a, b, c)의 상태이므로 a->c로 이동하게 됩니다.
그 후 마지막으로 hanoi(1, b, a, c)를 호출하는데, 이 함수또한 n==1이라 move(a, c)로 옮기려는데! 두번째 옮길 기둥이 b이고, 네번째 옮겨질 기둥이 c이므로 b->c로 이동을 하게 됩니다.
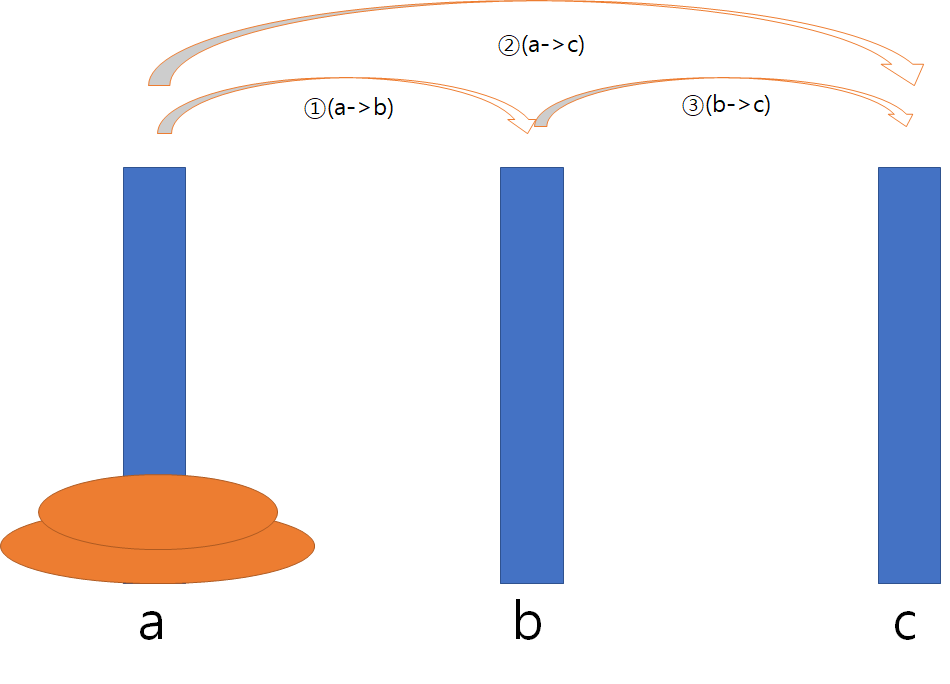
결과적으로 위와 같은 그림이 됩니다. 오.. 이게 돼?
마지막으로 n==3일 때를 살펴봅시다.
이번에도 n-1개를 b로 옮기고, 가장 큰 원판을 c로 옮기고 다시 b에 있는 모든 원판을 c로 옮기는 과정을 반복합시다. 점점 그림으로 그리기 벅차서 이번에는 코드가 진행되는 순서에 따라 호출하는 함수를 출력해 보았습니다.
hanoi(2, a, c, b) hanoi(1, a, b, c) move(a, c) :: basecase move(a, b) :: basecase hanoi(1, c, a, b) move(c, b) :: basecase move(a, c) :: basecase hanoi(2, b, a, c) hanoi(1, b, c, a) move(b, a) :: basecase move(b, c) :: basecase hanoi(1, a, b, c) move(a, c) :: basecase
위의 과정의 move()함수들만 떼어와서 움직이는것만 살펴보면 제대로 돌아가는걸 확인할 수 있습니다.
그렇습니다. n-1개를 a->b로 옮기고 남은 하나를 a->c로 옮기고 다시 n-1개를 b->c로 옮겨달라고 했더니 지가 알아서 해줍니다.
이런식으로 더 작은 부분들을 재귀적으로 처리하면 됩니다.
'알고리즘 문제풀이 > 백준' 카테고리의 다른 글
| 백준(boj) 2447 별 찍기 - 10(파이썬) (2) | 2020.07.31 |
|---|---|
| 백준(boj) 10870_피보나치 수5 (파이썬) (0) | 2020.07.29 |
| 백준(boj) 17140_이차원 배열과 연산 (파이썬, c++) (0) | 2020.04.24 |
| 백준(boj) 17142 연구소3 (파이썬, c++) (0) | 2020.04.23 |
| 백준(boj) 17144_미세먼지 안녕! (파이썬, c++) (0) | 2020.04.23 |